图

https://www.bilibili.com/video/BV1hg411V7Bm?p=62

1）图的分类

完全图

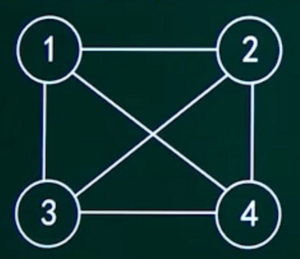
在无向图中，若每对顶点之间都有一条边相连，则称该图为完全图。

无向图完全图

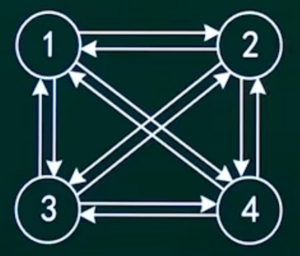
在有向图中，若每对顶点之间都有两条有向边相连接，则称该图为完全图。

有向图完全图

问题：n个顶点的无向图和有向图的完全图的边的个数为多少？

无向图

n个顶点：

顶点编号	边统计	参与的边
1	顶点1和顶点2 顶点1和顶点3 顶点1和顶点4 …… 顶点1和顶点n	n-1
2	顶点2和顶点3 顶点2和顶点4 …… 顶点2和顶点3 顶点2和顶点n	n-2
n-1	顶点n-1和顶点n	1
n	0

n-1，n-2，……，1，0

等差数列求和：(n-1+0)×n÷2=(n-1)×n÷2

有向图：

参考无线图，因为有向图两个顶点之间的线是两条，所以就是(n-1)×n

连通图

连通图：指任意两个顶点之间都有一个路径相连。

连通图与完全图不同的是：完全图中，任意两个顶点一定有至少一条边直接相连；而连通图中两个顶点之间的路径可以是间接相连的。