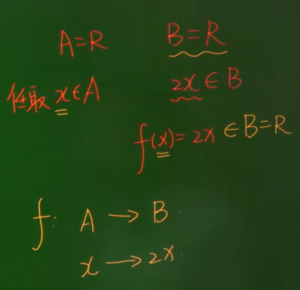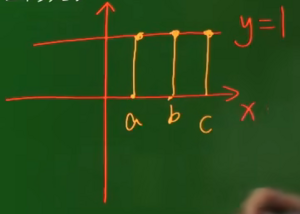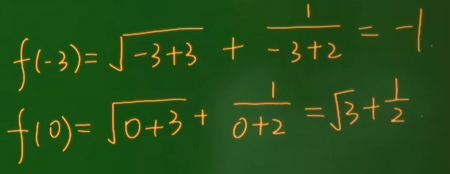“高中数学函数的概念”的版本间的差异
Jihongchang(讨论 | 贡献) |
Jihongchang(讨论 | 贡献) |
||
| (未显示同一用户的5个中间版本) | |||
| 第1行: | 第1行: | ||
| − | + | ||
1、函数的定义 | 1、函数的定义 | ||
| 第17行: | 第17行: | ||
1、设在一个变化过程中有两个变量 x 和 y,如果对于 x 的每一个值,y都有唯一的值与它对应,那么就说 x 是自变量,y 是 x 的函数。 | 1、设在一个变化过程中有两个变量 x 和 y,如果对于 x 的每一个值,y都有唯一的值与它对应,那么就说 x 是自变量,y 是 x 的函数。 | ||
| − | + | 2、将'''<big>自变量 x 取值的集合</big>'''叫做函数的'''<big>定义域</big>''',和自变量 x 的值对应的 '''<big>y 值叫做函数值</big>''','''<big>函数值</big>'''的集合叫做'''<big>函数的值域</big>'''。 | |
| + | |||
| + | 初中已经学过: | ||
| + | |||
| + | # 正比例函数 <math>y=kx(k\neq0)</math> | ||
| + | # 一次函数 <math>y=kx+b(k\neq0)</math> | ||
| + | # 反比例函数 <math>y=\frac{k}{x}(k\neq0)</math> | ||
| + | # 二次函数:<math>y=ax^2+bx+c(a\neq0)</math> | ||
| + | |||
| + | |||
| − | |||
| − | + | 二、讲解新课 | |
| − | + | ||
| − | + | 函数的有关概念 | |
| + | |||
| + | 定义:设A、B是'''<big>非空</big>'''的数集,如果按照某种确定的'''<big>对应关系f</big>''',使对于集合'''<big>A</big>'''中的'''<big>任意一个数x</big>''',在集合'''<big>B</big>'''中都'''<big>有唯一</big>'''确定的数 f(x) 和它对应,那么就称 '''<big>f:A->B为从集合A到集合B的一个函数</big>''', | ||
| + | |||
| + | 记作<math>y=f(x)</math>,<math>x\in A</math>。 | ||
| + | |||
| + | |||
| + | |||
| + | 注意:“在集合'''<big>B</big>'''中都'''<big>有唯一</big>'''确定的数 f(x) 和它对应”是指一个值x通过f(x)得到的也是一个值y,而不是多个值,而不是多个值;对应不同的x值得到的y值可以是相等的。 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | 例:[[文件:函数示例1.png|无|缩略图]] | ||
| + | |||
| + | |||
| + | |||
| + | 问题:<math>y=1(x\in R)</math>是函数吗? | ||
| + | |||
| + | 是 | ||
| + | [[文件:Y=1(x∈R).png|无|缩略图]]对应上面,疑问:<math>y=f(x)=\sqrt{x}(x>0,x\in R)</math> 是函数吗?毕竟y有正负两个取值 | ||
| + | |||
| + | |||
| + | 定义域(domain):'''<big>x的取值范围A</big>'''叫做函数的<big>'''定义域'''</big>;与x值对应的y值叫做'''<big>函数值</big>'''。 | ||
| + | |||
| + | 值域(range):'''<big>函数值的集合</big>''' | ||
| + | |||
| + | |||
| + | (二) | ||
| + | |||
| + | 关于求定义域及函数的值: | ||
| + | |||
| + | 例1、已知函数<math>f(x)=\sqrt{x+3}+\frac{1}{x+2}</math> | ||
| + | |||
| + | (1)求函数的定义域 | ||
| + | |||
| + | 解: | ||
| + | [[文件:求函数的定义域1.png|无|缩略图|600x600像素]] | ||
| + | |||
| + | |||
| + | (2)求f(-3),f(0)的值 | ||
| + | |||
| + | 解: | ||
| + | [[文件:求f(-3)和f(0).png|无|缩略图|450x450像素]] | ||
| + | |||
| + | |||
| + | (3)当a>0时,求f(a),f(a-1)的值。 | ||
| + | |||
| + | 解: | ||
| + | [[文件:求f(a)和f(a-1).png|无|缩略图|450x450像素]] | ||
2022年8月13日 (六) 07:27的最新版本
1、函数的定义
2、关于求定义域
3、函数的值与值域
4、函数的三要素判断同一函数
一、复习引入:
初中(传统)的函数的定义是什么?
1、设在一个变化过程中有两个变量 x 和 y,如果对于 x 的每一个值,y都有唯一的值与它对应,那么就说 x 是自变量,y 是 x 的函数。
2、将自变量 x 取值的集合叫做函数的定义域,和自变量 x 的值对应的 y 值叫做函数值,函数值的集合叫做函数的值域。
初中已经学过:
- 正比例函数 解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle y=kx(k\neq0)}
- 一次函数 解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle y=kx+b(k\neq0)}
- 反比例函数 解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle y=\frac{k}{x}(k\neq0)}
- 二次函数:解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle y=ax^2+bx+c(a\neq0)}
二、讲解新课
函数的有关概念
定义:设A、B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x) 和它对应,那么就称 f:A->B为从集合A到集合B的一个函数,
记作解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle y=f(x)} ,解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle x\in A} 。
注意:“在集合B中都有唯一确定的数 f(x) 和它对应”是指一个值x通过f(x)得到的也是一个值y,而不是多个值,而不是多个值;对应不同的x值得到的y值可以是相等的。
例:
问题:解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle y=1(x\in R)} 是函数吗?
是
对应上面,疑问:解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle y=f(x)=\sqrt{x}(x>0,x\in R)} 是函数吗?毕竟y有正负两个取值
定义域(domain):x的取值范围A叫做函数的定义域;与x值对应的y值叫做函数值。
值域(range):函数值的集合
(二)
关于求定义域及函数的值:
例1、已知函数解析失败 (带SVG或PNG备选的MathML(建议用于现代的浏览器和辅助工具):从服务器“https://wikimedia.org/api/rest_v1/”返回无效的响应(“Math extension cannot connect to Restbase.”):): {\displaystyle f(x)=\sqrt{x+3}+\frac{1}{x+2}}
(1)求函数的定义域
解:
(2)求f(-3),f(0)的值
解:
(3)当a>0时,求f(a),f(a-1)的值。
解: