“树的遍历”的版本间的差异

来自姬鸿昌的知识库
跳到导航 跳到搜索
 
（未显示同一用户的4个中间版本）
第53行： 第53行：
 
|-
 
|-
 
|E、D
 
|E、D
−
|
+
| 
 
|}
 
|}
 
在以F为根结点的左子树中，前序序列是DE，中序序列是ED，那么D是根结点，E是左叶子结点
 
在以F为根结点的左子树中，前序序列是DE，中序序列是ED，那么D是根结点，E是左叶子结点
第60行： 第60行：
 
|-
 
|-
 
|E
 
|E
−
|
+
| 
 
|}
 
|}
 
在以A为根结点的右子树中，前序序列是CG，中序序列是GC，那么C是根结点，G在以C为根结点的树中的左子树中
 
在以A为根结点的右子树中，前序序列是CG，中序序列是GC，那么C是根结点，G在以C为根结点的树中的左子树中
第67行： 第67行：
 
|-
 
|-
 
|G
 
|G
−
|
+
| 
 
|}
 
|}
 
以上子树合并起来就是
 
以上子树合并起来就是
第79行： 第79行：
 
! colspan="3" |F
 
! colspan="3" |F
 
!G
 
!G
−
!
+
! 
 +
|-
 +
! 
 +
! colspan="2" |D
 +
! 
 +
! 
 +
! 
 +
|-
 +
! 
 +
!E
 +
! 
 +
! 
 +
! 
 +
! 
 +
|}
 +
 
 +
 
 +
 
 +
=== 考点1：二叉树的遍历方式 ===
 +
对下图所示的二叉树进行中序遍历（左子树，根结点，右子树）的结果是（）。
 +
[[文件:二叉树的遍历方式考点1.png|无|缩略图]]
 +
A、523461
 +
 
 +
B、253416
 +
 
 +
C、246531
 +
 
 +
D、254361  √
 +
 
 +
 
 +
=== 考点2：由前序、中序遍历序列构造二叉树 ===
 +
某二叉树的先序遍历序列为ABCDFGE，中序遍历序列为BAFDGCE。
 +
 
 +
以下关于该二叉树的叙述中，正确地是（）。
 +
 
 +
A、该二叉树的高度（层数）为4  √
 +
 
 +
B、该二叉树结点D是叶子结点
 +
 
 +
C、该二叉树是满二叉树（即每层的结点数达到最大值）
 +
 
 +
D、该二叉树有5个叶子结点
 +
 
 +
解：
 +
 
 +
根据先序序列ABCDFGE和后续序列BAFDGCE构造二叉树
 +
{| class="wikitable"
 +
! colspan="2" |A
 +
|-
 +
|B
 +
|F、D、G、C、E
 +
|}
 +
{| class="wikitable"
 +
! colspan="2" |C
 
|-
 
|-
−
!
+
|F、D、G
 +
|E
 +
|}
 +
{| class="wikitable"
 
! colspan="2" |D
 
! colspan="2" |D
 +
|-
 +
|F
 +
|G
 +
|}
 +
合并以上子树得到
 +
{| class="wikitable"
 +
! colspan="5" |A
 +
|-
 +
! colspan="2" |B
 +
! colspan="3" |C
 +
|-
 
!
 
!
 
!
 
!
−
!
+
! colspan="2" |D
 +
!E
 
|-
 
|-
−
!
 
−
!E
 
−
!
 
 
!
 
!
 
!
 
!
 +
!F
 +
!G
 
!
 
!
 
|}
 
|}
 +
高度为4；
 +
 +
D不是叶子结点；
 +
 +
不是满二叉树；
 +
 +
有4个叶子结点；

2022年9月19日 (一) 07:12的最新版本

https://www.bilibili.com/video/BV1hg411V7Bm?p=60

1）二叉树的遍历方式

前序/先序遍历：先遍历根结点，然后遍历左子树，最后遍历右子树。根、左、右

中序遍历：先遍历左子树，然后遍历根结点，最后遍历右子树。 左、根、右

后序遍历：先遍历左子树，然后遍历右子树，最后遍历根结点。左、右、根

层序遍历：从上往下逐层遍历。上到下、左到右

二叉树的遍历方式.png

图中前序遍历结果是？

1、2、4、5、7、8、3、6

图中中序遍历结果是？

4、2、7、8、5、1、3、6

图中后序遍历结果是？

4、8、7、5、2、6、3、1

图中层序遍历结果是？

1、2、3、4、5、6、7、8


2）由前序、中序遍历序列构造二叉树

由前序序列为ABHFDECG；中序序列为HBEDFAGC构造二叉树；

构造二叉树.png

解题思路：

根据前序序列的规则（先遍历根结点，然后遍历左子树，再遍历右子树）得到子树的根结点，再根据中序序列中根结点出现的位置把序列分为左子树跟右子树两部分。

依据前序序列ABHFDECG先遍历根结点，然后遍历左子树，再遍历右子树，得知A是根节点，又有中序序列HBEDFAGC先遍历左子树，然后遍历根结点，最后遍历右子树，得知H、B、E、D、F在A为根节点的树的左子树中，G、C在A为根节点的树的右子树中

A
H、B、E、D、F GC

其中左子树中，前序序列为BHFDE，那么B是根结点，中序序列HBEDF，以B为根结点拆成H和E、D、F一个左子树，一个右子树

B
H E、D、F

以B为根结点的右子树中，前序序列FDE，中序序列EDF，那么F是根结点，E、D都在以F为根结点的左子树中

F
E、D  

在以F为根结点的左子树中，前序序列是DE，中序序列是ED，那么D是根结点，E是左叶子结点

D
E  

在以A为根结点的右子树中，前序序列是CG，中序序列是GC，那么C是根结点，G在以C为根结点的树中的左子树中

C
G  

以上子树合并起来就是

A
B C
H F G  
  D      
  E        


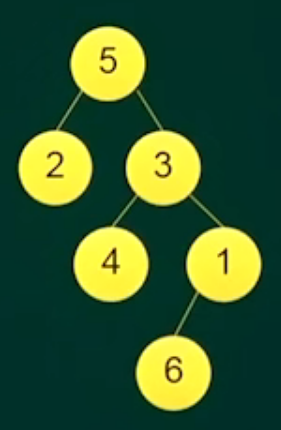
考点1：二叉树的遍历方式

对下图所示的二叉树进行中序遍历（左子树，根结点，右子树）的结果是（）。

二叉树的遍历方式考点1.png

A、523461

B、253416

C、246531

D、254361 √


考点2：由前序、中序遍历序列构造二叉树

某二叉树的先序遍历序列为ABCDFGE，中序遍历序列为BAFDGCE。

以下关于该二叉树的叙述中，正确地是（）。

A、该二叉树的高度（层数）为4 √

B、该二叉树结点D是叶子结点

C、该二叉树是满二叉树（即每层的结点数达到最大值）

D、该二叉树有5个叶子结点

解：

根据先序序列ABCDFGE和后续序列BAFDGCE构造二叉树

A
B F、D、G、C、E
C
F、D、G E
D
F G

合并以上子树得到

A
B C
D E
F G

高度为4；

D不是叶子结点；

不是满二叉树；

有4个叶子结点；

取自“https://www.jihongchang.top/index.php?title=树的遍历&oldid=2094”