“初级程序员 2020年 下半年 下午”的版本间的差异
跳到导航
跳到搜索
Jihongchang(讨论 | 贡献) (建立内容为“=== 第1题 === 下面流程图所示算法的功能是:在一个二进制位串中,求出连续的“1”构成的所有子串的最大长度M。 文件:…”的新页面) |
Jihongchang(讨论 | 贡献) (→第1题) |
||
| 第7行: | 第7行: | ||
在对各个二进制位扫描的过程中,变量L动态地记录连续“1”的个数。 | 在对各个二进制位扫描的过程中,变量L动态地记录连续“1”的个数。 | ||
| + | |||
| + | 答案: | ||
| + | |||
| + | (1)0 | ||
| + | |||
| + | (2)L+1或等效形式 | ||
| + | |||
| + | (3)0→L或等效形式 | ||
| + | |||
| + | (4)L>M或L≥M或等效形式 | ||
| + | |||
| + | (5)M | ||
解析: | 解析: | ||
| − | + | 本流程图采用的算法是对二进制位串从左到右进行逐位判断,并累计连续遇到数字1的个数L,再以动态地得到当前L的最大值M。 | |
| + | |||
| + | 初始时,L和M都应该是0,故初值为0,因此,流程图的空(1)处应填0。 | ||
| + | |||
| + | |||
| + | 接着开始对i=1,2,...,n循环,一次判断二进制数位A[i]是否为1。 | ||
| + | |||
| + | 如果A[i]=1,就应该将L增1,即执行L+1→L,因此流程图的空(2)处应填L+1; | ||
| + | |||
| + | 如果A[i]=0,则应该将数字1的累计长度L清0,重新开始累计,因此,流程图的空(3)处应填0→L。 | ||
| + | |||
| + | |||
| + | 当遇到数字L进行累计后,应将L与现行的擂台值M进行比较。 | ||
| + | |||
| + | 如果L>M,则显然应该以新的L值代替原来的M值,即执行L→M; | ||
| − | + | 如果L<M,则不能更新M值; | |
| − | + | 如果L=M,则可以更新也可以不更新M值,对计算结果没有影响。 | |
| − | + | 为此,流程图的空(4)处可填L>M或L≥M(填前者更好),而空(5)处应填M。 | |
2022年10月7日 (五) 03:59的版本
第1题
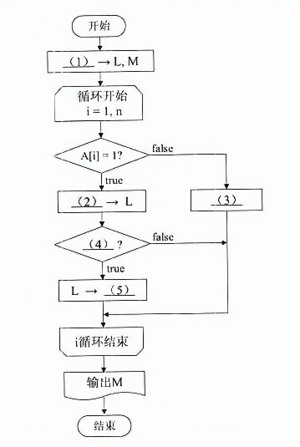
下面流程图所示算法的功能是:在一个二进制位串中,求出连续的“1”构成的所有子串的最大长度M。
例如,对于二进制位串0100111011110,M=4。
该算法中,将长度为n的二进制位串的各位数字,按照从左到右的顺序依次存放在数组A[1..n]。
在对各个二进制位扫描的过程中,变量L动态地记录连续“1”的个数。
答案:
(1)0
(2)L+1或等效形式
(3)0→L或等效形式
(4)L>M或L≥M或等效形式
(5)M
解析:
本流程图采用的算法是对二进制位串从左到右进行逐位判断,并累计连续遇到数字1的个数L,再以动态地得到当前L的最大值M。
初始时,L和M都应该是0,故初值为0,因此,流程图的空(1)处应填0。
接着开始对i=1,2,...,n循环,一次判断二进制数位A[i]是否为1。
如果A[i]=1,就应该将L增1,即执行L+1→L,因此流程图的空(2)处应填L+1;
如果A[i]=0,则应该将数字1的累计长度L清0,重新开始累计,因此,流程图的空(3)处应填0→L。
当遇到数字L进行累计后,应将L与现行的擂台值M进行比较。
如果L>M,则显然应该以新的L值代替原来的M值,即执行L→M;
如果L<M,则不能更新M值;
如果L=M,则可以更新也可以不更新M值,对计算结果没有影响。
为此,流程图的空(4)处可填L>M或L≥M(填前者更好),而空(5)处应填M。