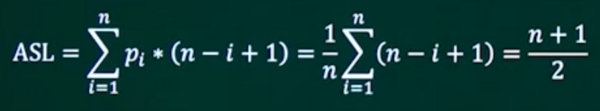“查找”的版本间的差异
Jihongchang(讨论 | 贡献) |
Jihongchang(讨论 | 贡献) |
||
| 第111行: | 第111行: | ||
| | | | ||
|} | |} | ||
| + | |||
| + | |||
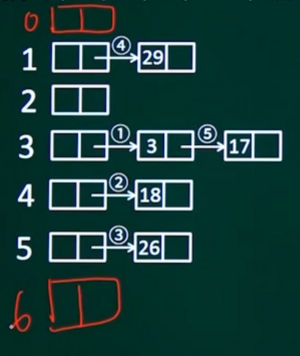
=== 3)散列表查找:拉链法 === | === 3)散列表查找:拉链法 === | ||
关键码为(3,18,26,29,17),散列函数h=key%7,用链地址法。 | 关键码为(3,18,26,29,17),散列函数h=key%7,用链地址法。 | ||
[[文件:散列表查找 拉链法.png|无|缩略图]] | [[文件:散列表查找 拉链法.png|无|缩略图]] | ||
| + | |||
| + | |||
| + | === 考点1:二分法查找的条件 === | ||
| + | 在一个线性表上可以进行二分查找(折半查找)的充分必要条件是()。 | ||
| + | |||
| + | A、线性表采用顺序存储且元素有序排列 √ | ||
| + | |||
| + | B、线性表采用顺序存储且元素无序排列 | ||
| + | |||
| + | C、线性表采用单链表存储且元素有序排列 | ||
| + | |||
| + | D、线性表采用单链表存储且元素无序排列 | ||
2022年9月21日 (三) 08:29的版本
https://www.bilibili.com/video/BV1hg411V7Bm?p=65
1)顺序查找
顺序查找:将待查找的关键字跟表中的数据从头至尾按顺序进行比较。
平均查找长度(等概率情况):
2)二分法查找
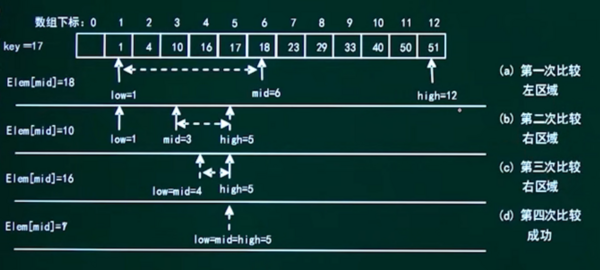
二分法查找(折半查找)的基本思想是:(设R[low,...,high]是当前的查找区)
(1)确定该区间的中点位置:mid=⌊(low+high)/2⌋(向下取整);
(2)将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下。
- 若R[mid].key>k,则由表的有序性可知R[mid,...,n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low,...,mid-1]中。因此,新的查找区间是左子表R[low,...,high],其中high=mid-1。
- 若R[mid].key<k,则要查找的k必在mid的右子表R[mid+1,...,high]中,即新的查找区间是右子表R[low,...,high],其中low=mid+1。
- 若R[mid].key=k,则查找成功,算法结束。
(3)下一次查找是针对新的查找区间进行,重复步骤(1)和(2)。
(4)在查找过程中,low逐步增加,而high逐步减少。如果high<low,则查找失败,算法结束。
请给出在含有12个元素的有序表{1,4,10,16,17,18,23,29,33,40,50,51}中二分查找关键字17的过程。
折半查找在查找成功时关键字的比较次数最多为⌊log2n⌋+1次。
折半查找的时间复杂度为O(log2n)次。
折半查找仅适用于元素有序的顺序表。
2)二分法查找(循环法)
int biSearch(int r[], int low, int high, int key)
{
//r[low...high]中的元素按非递减顺序排列,用二分查找法在数组r中查找与key相同的元素,若找到则返回该元素在数组r的下标,否则返回-1
int mid;
while(low <= high)
{
mid = (low + high)/2;
if(key == r[mid]) return mid;
else if (key < r[mid]) high = mid - 1;
else low = mid + 1;
}//end while
return -1;
}//end biSearch
https://www.bilibili.com/video/BV1hg411V7Bm?p=66
2)二分法查找(递归法)
int biSearch_rec(int r[], int low, int high, int key)
{
//r[low...high]中的元素按非递减顺序排列,用二分查找法在数组r中查找与key相同的元素,若找到则返回该元素在数组r的下标,否则返回-1
int mid;
if(low <= high)
{
mid = (low + high)/2;
if(key == r[mid]) return mid;
else if (key < r[mid]) return biSearch_rec(r, low, mid-1, key);
else return biSearch_rec(r, mid + 1, high, key);
}//end if
return -1;
}//end biSearch_rec
3)散列表查找:线性探查法
散列表查找的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0..n-1](n<m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。
关键码为(3,18,26,29,17),存储空间为10,散列函数h=key%7。取余结果相同就会发生冲突,发生冲突之后就往后面最近的一个空闲空间中。
比如存放17时:因为3%7=3,先放入了3的位置,17%7=3就只能往后放在后面最近的一个空闲空间6中了。
| 地址空间 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 存储元素值 | 29 | 3 | 18 | 26 | 17 |
3)散列表查找:拉链法
关键码为(3,18,26,29,17),散列函数h=key%7,用链地址法。
考点1:二分法查找的条件
在一个线性表上可以进行二分查找(折半查找)的充分必要条件是()。
A、线性表采用顺序存储且元素有序排列 √
B、线性表采用顺序存储且元素无序排列
C、线性表采用单链表存储且元素有序排列
D、线性表采用单链表存储且元素无序排列