特殊二叉树
https://www.bilibili.com/video/BV1hg411V7Bm?p=61
1)二叉查找树
二叉排序/查找树
左子树小于根
右子树大于根
对每一个结点而言,它的左孩子小于它自身,右孩子大于它自身。
特点:
1)二叉查找树的中序遍历序列为从小到大排列的序列。
2)值最小的结点无左子树,值最大的结点无右子树。
3)每一层从左到右进行遍历的序列为从小到大排列的序列。
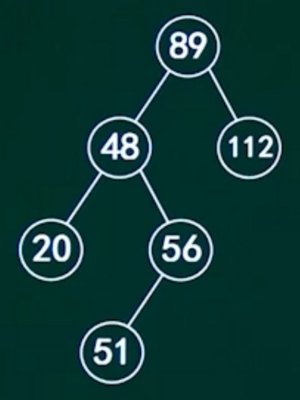
插入结点:序列(89,48,56,48,20,112,51)
1、若查找二叉树为空树,则以新结点为查找二叉树;
2、将要插入结点值与父结点值比较,确定要放左子树还是右子树中,若子树为空,则作为子树的根结点插入;
3、若该键值结点已存在,则不再插入。
二叉查找树为空树,以新结点89为查找二叉树
| 89 |
|---|
将要插入结点值48与父结点值89比较,48<89,放左子树,左子树为空,作为子树的根结点插入;
| 89 | |
|---|---|
| 48 | |
将要插入结点值56与根结点值89比较,56<89,放左子树;
左子树不为空,将要插入结点值56与左子树的根结点值48比较,56>48,放右子树;
右子树为空,作为右子树的根结点插入;
| 89 | ||
|---|---|---|
| 48 | ||
| 56 | ||
键值48的结点已存在,不再插入
| 89 | |||
|---|---|---|---|
| 48 | |||
| 56 | |||
将要插入结点值20与根结点值89比较,20<89,放左子树;
左子树不为空,将要插入结点值20与左子树的根结点值48比较,20<48,放左子树;
左子树为空,作为左子树的根结点插入;
| 89 | |||
|---|---|---|---|
| 48 | |||
| 20 | 56 | ||
将要插入结点值112与根结点值89比较,112>89,放右子树;
右子树为空,作为右子树的根结点插入;
| 89 | |||
|---|---|---|---|
| 48 | 112 | ||
| 20 | 56 | ||
将要插入结点值51与根结点值89比较,51<89,放左子树;
左子树不为空,将要插入结点值51与左子树的根结点值48比较,51>48,放右子树;
右子树不为空,将要插入结点值51与右子树的根结点值56比较,51<56,放左子树;
左子树为空,作为左子树的根结点插入;
| 89 | ||||
|---|---|---|---|---|
| 48 | 112 | |||
| 20 | 56 | |||
| 51 | ||||
2)哈夫曼树
需要了解的基本概念:
树的路径长度:从树根到树中每一结点的路径长度之和(一般讨论的对象是叶子结点)
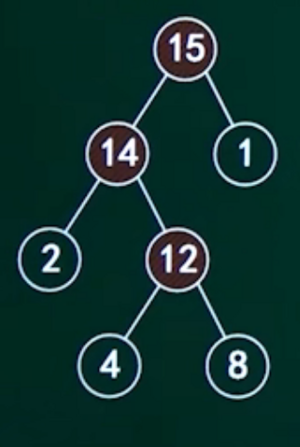
比如图1中:
2到根15距离是2;
4到根15距离是3;
8到根15距离是3;
1到根15距离是1;
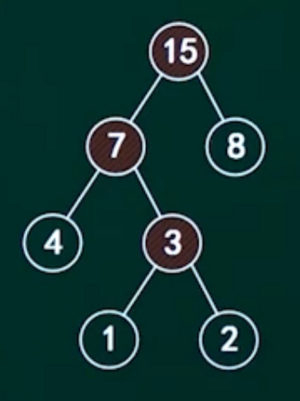
图2中:
4到根15距离是2;
1到根15距离是3;
2到根15距离是3;
8到根15距离是1;
权:在一些应用中,赋予树中结点的一个有某种意义的实数(一般讨论的对象是叶子结点)
结点值就是叶子结点的权,比如图1中:
2的权就是2,4的权就是4……
带权路径长度:结点到树根之间的路径长度与该结点上权的乘积
比如图1中:
2的带权路径长度就是2×2;
4的带权路径长度就是3×4;
8的带权路径长度就是3×8;
1的带权路径长度就是1×1;
树的带权路径长度(树的代价):树中所有叶结点的带权路径长度之和
比如图1就是:
2×2+3×4+3×8+1×1
=4+12+24+1
=16+25
=41;
图2就是:
2×4+3×1+3×2+1×8
=8+3+6+8
=11+14
=25;
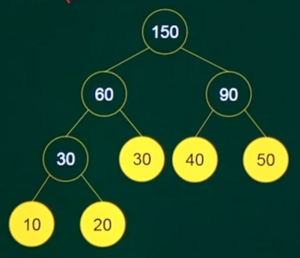
例:假设有一组权值50,20,30,40,10,请尝试构造哈夫曼树。(如何构造代价最小的哈夫曼树)
从找权值最小的两个叶子结点构建子树开始,循环
考点1:二叉排序树的性质
对一棵二叉排序树进行()遍历,可得到该二叉树中结点关键字的有序序列。
A、先序
B、中序 √
C、后序
D、层序
解:二叉排序树的特点是:左孩子结点值<父结点<右孩子结点,
中序遍历就是左、中、右的顺序;
而先序遍历是中、左、右的顺序,并不满足有序
考点2:二叉排序树的构造
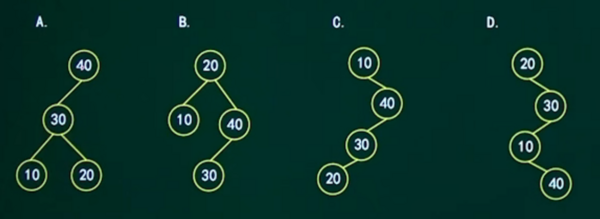
设有关键码序列(10,40,30,20),根据该序列构建的二叉排序树是()。
解:
第一个是根节点肯定是10,所以选项C
考点3:哈夫曼树
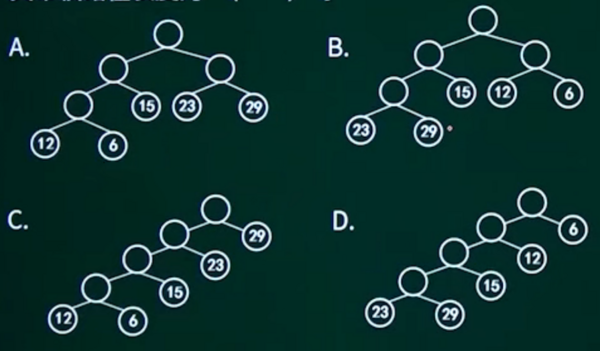
由权值为29、12、15、6、23的5个叶子结点构造的哈夫曼树为(),
解:
1、取权值最小的两个值作为叶子结点组成一棵子树(这样做是为了最小化路径最远的结点权值)
| 18 | |
| 6 | 12 |
|---|---|
2、循环找最小的权值组成子树
| 33 | ||
| 18 | 15 | |
|---|---|---|
| 6 | 12 | |
然后剩下两个结点23、29,作为二叉树就只能并列放在第2层,这样能使剩下的大权值结点距离根相加最近、又能同时放得下2个结点
| 85 | ||||
| 33 | 52 | |||
| 18 | 15 | 23 | 29 | |
|---|---|---|---|---|
| 6 | 12 | |||
所以是图A。
其带权路径长度为()。
| A、85 | B、188 | C、192 | D、222 |
解:计算图A的带权路径长度:
3×6+3×12+2×15+2×23+2×29
=3×18+30+2×52
=54+30+104
=84+104
=188
答案:B