图

https://www.bilibili.com/video/BV1hg411V7Bm?p=62

1）图的分类

完全图

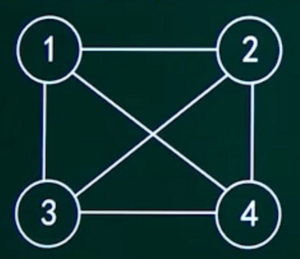
在无向图中，若每对顶点之间都有一条边相连，则称该图为完全图。

无向图完全图

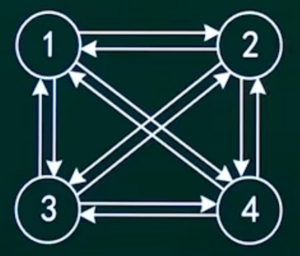
在有向图中，若每对顶点之间都有两条有向边相连接，则称该图为完全图。

有向图完全图

问题：n个顶点的无向图和有向图的完全图的边的个数为多少？

无向图

n个顶点：

顶点编号	边统计	参与的边
1	顶点1和顶点2 顶点1和顶点3 顶点1和顶点4 …… 顶点1和顶点n	n-1
2	顶点2和顶点3 顶点2和顶点4 …… 顶点2和顶点3 顶点2和顶点n	n-2
n-1	顶点n-1和顶点n	1
n	0

n-1，n-2，……，1，0

等差数列求和：(n-1+0)×n÷2=(n-1)×n÷2

有向图：

参考无线图，因为有向图两个顶点之间的线是两条，所以就是(n-1)×n

连通图

连通图：指任意两个顶点之间都有一个路径相连。

连通图与完全图不同的是：完全图中，任意两个顶点一定有至少一条边直接相连；而连通图中两个顶点之间的路径可以是间接相连的。

在有向图中，如果可以直接满足任意两个顶点之间都有一个路径相连的条件的叫做强连通图；如果不计较方向可以直接满足任意两个顶点之间都有一个路径相连的条件的叫做弱连通图。

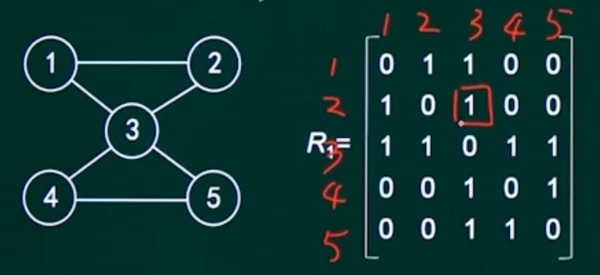
2）图的转换：无向图转邻接矩阵

用一个n阶方阵R来存放图中各结点的关联信息，其矩阵元素R_ij定义为：

无向图转换的邻接矩阵为对称矩阵。