初级程序员 2020年 下半年 下午

第1题

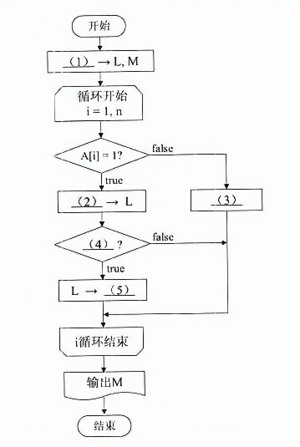
下面流程图所示算法的功能是：在一个二进制位串中，求出连续的“1”构成的所有子串的最大长度M。

例如，对于二进制位串0100111011110，M=4。

该算法中，将长度为n的二进制位串的各位数字，按照从左到右的顺序依次存放在数组A[1..n]。

在对各个二进制位扫描的过程中，变量L动态地记录连续“1”的个数。

答案：

（1）0

（2）L+1或等效形式

（3）0→L或等效形式

（4）L>M或L≥M或等效形式

（5）M

解析：

本流程图采用的算法是对二进制位串从左到右进行逐位判断，并累计连续遇到数字1的个数L，再以动态地得到当前L的最大值M。

初始时，L和M都应该是0，故初值为0，因此，流程图的空（1）处应填0。

接着开始对i=1，2，...，n循环，一次判断二进制数位A[i]是否为1。

如果A[i]=1，就应该将L增1，即执行L+1→L，因此流程图的空（2）处应填L+1；

如果A[i]=0，则应该将数字1的累计长度L清0，重新开始累计，因此，流程图的空（3）处应填0→L。

当遇到数字L进行累计后，应将L与现行的擂台值M进行比较。

如果L>M，则显然应该以新的L值代替原来的M值，即执行L→M；

如果L<M，则不能更新M值；

如果L=M，则可以更新也可以不更新M值，对计算结果没有影响。

为此，流程图的空（4）处可填L>M或L≥M（填前者更好），而空（5）处应填M。

第2题

阅读以下说明和C代码，填补C代码中的空缺，将解答写在答题纸的对应栏内。

【说明】

答案：

（1）fabs(x)<=1e-6

（2）x2

（3）x/(x1*x1)

（4）(x2-x1)/x1

（5）x+=0.1

解析：

本题考查C程序基本运算和流程控制的应用。

函数cubeRoot(x)根据给定的公式计算x的立方根。

根据精度要求，绝对值小于1e-6的数，其立方根为0，因此，空（1）处填入“fabs(x)<=1e-6”或其等效形式。

分析函数cubeRoot中的代码，可知x1对应公式中的x_n，x2对应公式中的x_n+1，每次循环时，需要将x2传给x1，再计算出新的x2，因此空（2）处应填入“x2”，

空（3）处应填入“x/(x1*x1)”。

在满足精度要求时结束循环，即空（4）处应填入“(x2-x1)/x1”。

根据题干部分的说明，显然空（5）处应填入“x+=0.1”或其等效形式。

#include<stdio.h>
#include<math.h>

/*
* 
*/
double cubeRoot(double x) {
	double x1, x2 = x;

	printf("x1=%f, x2=%f", x1, x2);

	if (fabs(x) <= 1e-6) return 0.0;

	do {
		x1 = x;
		x2 = (2.0 * x1 + x / x1 * x1);

	} while ( fabs(  (x2 - x1) / x1 ) >= 1e-6 );

	return x2;

}

int main()
{
	double x;
	for (x = -8.0; x <= 8.0; (x += 0.1))
		printf("cube_root(%.1f)=%.4f\n", x, cubeRoot(x));
	return 0;
}