有限自动机和正规式

https://www.bilibili.com/video/BV1hg411V7Bm?p=50

1）正规式

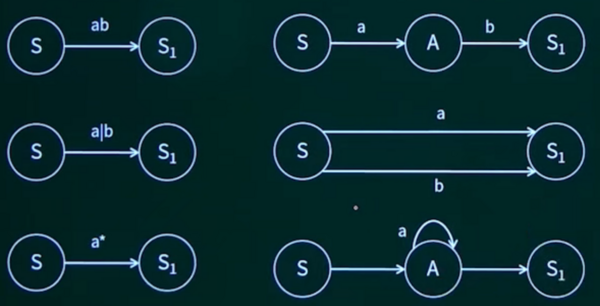
正规式：由正规文法转换而来，通常正规文法等价于正规式。

	文法产生式	正规式
规则1	A→xB,B→y	A=xy
规则2	A→xA|y	A=x*y
规则3	A→x,A→y	A=x|y

说明：

规则1不难理解，由A可以推导出xB，又由B可以推导出y，那么就可以根据前面两点推导出A=xy；

规则2：A=x^*y中的“^*”表示出现0次或任意次

A→xA|y表示——由A可以推导出xA，也可以由A推导出y

由A→y，则x出现0次；

又由A→xA和A→y，可以得到A→xy，则x出现了1次；

又由A→xA和A→xy，可以得到A→xxy，则x出现了2次；

...

又由A→x...A和A→xy，可以得到A→xx...y，则x出现了N次；

正规集：正规文法产生的集合是语言基本字符集上的字符串的一个子集。

正规式	正规集
ab	符号串ab构成的集合	a、b
a|b	符号串a、b构成的集合
a*	由0个或多个a构成的符号串集合
(a|b)*	所有由a和b构成的符号串集合	(a|b)(a|b) aa、ab、ba、bb
a(a|b)*	a为首字符的a和b构成的符号串集合
(a|b)*abc	a和b构成的以abb结尾的符号串集合

表示“以字符a开头且仅由字符a、b构成的所有字符串”的正规式为（）。

A、a^*b^*

B、(a|b)^*a

C、a(a|b)^* √

D、(ab)^*

题解：

因为“^*”表示出现0次或多次，

那么对于选项A，如果a出现0次就变成了以字符b开头；

对于选项B，也可以是以字符b开头，

选项D，会是ab、abab、ababab，所以选C

2）有限自动机

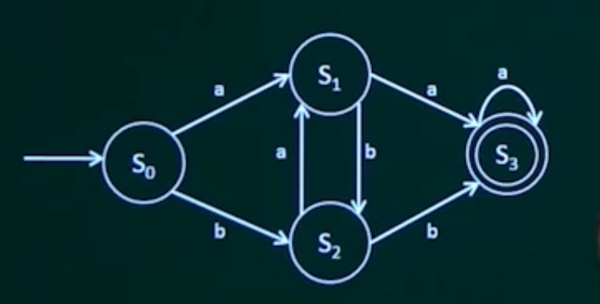
下图所示的有限自动机中，S₀是初始状态，S₃为终止状态，该自动机不能识别（）。

A、abab √

B、aaaa

C、babb

D、abba

题解：

一定要初始状态开始，终止状态结束。

选项A的状态路径是S₀→S₁→S₂→S₁→S₂，没有到达终止状态；

选项B的状态路径是S₀→S₁→S₃→S₃→S₃，到达终止状态结束；

选项C的状态路径是S₀→S₂→S₁→S₂→S₃，到达终止状态结束；

选项D的状态路径是S₀→S₁→S₂→S₃→S₃，到达终止状态结束；

所以答案是选项A

考点1：正规式

正规式(ab|c)(0|1|2)表示的正规集合中有（）个元素，

A、3

B、5

C、6 √

D、9

（）是该正规集中的元素。

A、abc012

B、a0

C、c02

D、c0 √

题解：

正规式(ab|c)(0|1|2)表示的正规集合是：

ab0、ab1、ab2

c0、c1、c2

考点2：有限自动机

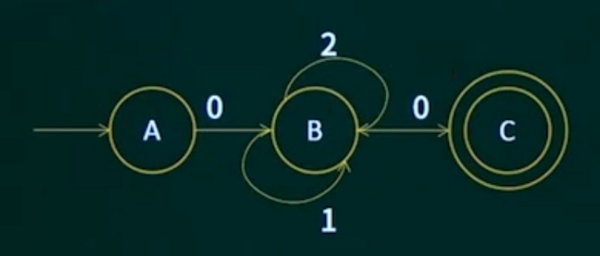
下图是一个有限自动机的状态转换图（A为初态、C为终态），该自动机识别的字符串集合可用正规式（）来表示。

A、(1|2)^*00

B、0(1|2)^*0 √

C、(0|1|2)^*

D、00(1|2)^*

题解：

注意：没有C回指B方向的线，那个箭头是2那条方向线的箭头