矩阵

https://www.bilibili.com/video/BV1hg411V7Bm?p=56

1）特殊矩阵

上三角矩阵、下三角矩阵、对角矩阵、对称矩阵都是方阵，行数、列数相同。

2）非特殊矩阵

稀疏矩阵：

非零元素的个数远远少于零元素的个数，且非零元素的分布没有规律。

对于稀疏矩阵，存储非零元素时必须同时存储其位置（即行号和列号），所以三元组(i, j, a_ij)可唯一确定矩阵中的一个元素。

三元组表为：(1, 2, 12)，(1, 4, 9)，(2 4, 7)，(3, 1, 1)，(4, 1, 2)，(4, 4, 1)。

3）矩阵的乘法

矩阵的乘法运算：

设A为m*p的矩阵，B为p*n的矩阵，那么m*n的矩阵C为矩阵A与B的乘积，记作C=AB，其中矩阵C中的第i行第j列元素可以表示为：

如下图所示：

说明：

第一行×第一列，然后再相加

A(行)×B(列)

A的i行×B的j列=C_ij

https://www.bilibili.com/video/BV1hg411V7Bm?p=57

考点：矩阵的乘法计算

f(1)=1，f(2)=1，n>2时f(n)=f(n-1)+f(n-2)。

据此可以导出，n>1时，有向量的递推关系式：(f(n+1), f(n))=(f(n), f(n-1))A

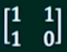
其中A是2*2矩阵（）。

从而，(f(n+1), f(n)=(f(2), f(1))*（）。

A、A^n-1

B、Aⁿ

C、Aⁿ⁺¹

D、Aⁿ⁺²

题解：

第一空

根据题意“f(1)=1，f(2)=1，n>2时f(n)=f(n-1)+f(n-2)”有

f(1)=1，f(2)=1，f(3)=f(3-1)+f(3-2)=f(2)+f(1)，f(4)=f(4-1)+f(4-2)=f(3)+f(2)....

f(1)	f(2)	f(3)	f(4)	...
1	1	f(2)+f(1) =1+1 =2	f(3)+f(2) =2+1 =3	...

得到当n>2时，n的值等于前两项之和（斐波那契数列），

又有“向量的递推关系式：(f(n+1), f(n))=(f(n), f(n-1))*A”，

分别将选项代入计算，以选项A为例

又有f(n)+f(n-1)=f(n+1)（任何一项都是前两项之和），得到

(f(n), f(n-1))×选项A=(f(n-1), f(n+1))，并不等于(f(n+1), f(n))，所以正确答案不是选项A，以此类推，正确答案是D。

第二空

生成缩略图出错：无法将缩略图保存到目标地点

我没听明白，我觉得视频也没讲明白

总结

矩阵

• 特殊矩阵
  • 三角矩阵
  • 对角矩阵
  • 对称/反对称矩阵
• 非特殊矩阵
  • 稀疏矩阵
• 矩阵乘法
  • 行*列