选择类排序
跳到导航
跳到搜索
5)直接选择类排序
https://www.bilibili.com/video/BV1hg411V7Bm/?p=70
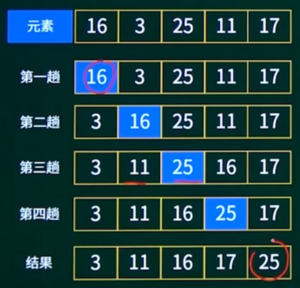
过程:首先在所有记录中选出排序码最小的记录,把它与第1个记录交换,然后再其余的记录内选出排序码最小的记录,与第2个记录交换......依次类推,直到所有记录排完为止。
void selectSort(int data[], int n)
{
//对data[0]~data[n-1]中的n个整数按非递减有序的方式进行排列
int i,j,k;
int temp;
for(i = 0; i < n - 1; i++)
{
for(k = i, j = i + 1; j < n; j++) //k表示data[i]~data[n-1]中最小元素的下标
{
if(data[j] < data[k]) {
k = j;
}
if(k!=i){
//将本趟找出的最小元素与data[i]交换
temp=data[i];
data[i]=data[k];
data[k]=temp;
}
}//end inner for
}//end outter for
}
4)堆排序
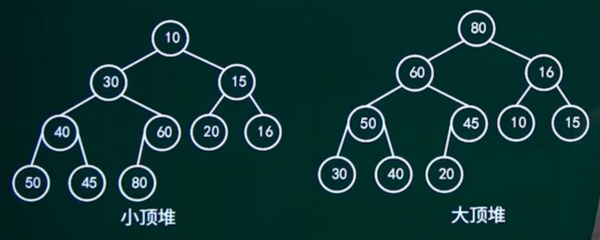
设有n个元素的序列{K1,K2,...,Kn},当且仅当满足下述关系之一时,称之为堆。
(1)Ki≤K2i且Ki≤K2i+1;(父结点总是小于孩子结点)
(2)Ki≥K2i且Ki≥K2i+1。(父结点总是大于孩子结点)
其中(1)称为小顶堆/小根堆,(2)称为大顶堆/大根堆
堆排序的时间复杂度为:O(nlog2n)
考点:大顶堆和小顶堆
对于n个元素的关键字序列{K1,K2,...,Kn},当且仅当满足Ki≤K2i且Ki≤K2i+1(1<i<n/2),则称该序列为小顶堆。
若将其中的“≤”换为“≥”则称其为大顶堆。
由此可知,()是大顶堆。
A、7,2,3,4,5,6,1
B、7,5,4,2,6,3,1
C、7,6,4,2,5,3,1 √
D、7,5,3,1,6,4,2
解:
选项中的数列就是0,1,2,3,4,5,6作为i参数,按4个选项中的序列顺序画树,看哪个符合大顶堆的定义:Ki≥K2i且Ki≥K2i+1
A
| 7 | ||
|---|---|---|
| 2 | 3 | |
| 4 | ||
2作为4的父结点却小于4,所以不是大顶堆。
B
| 7 | ||
|---|---|---|
| 5 | 4 | |
| 2 | 6 | |
5作为6的父结点却小于6,所以不是大顶堆。
C
| 7 | |||
|---|---|---|---|
| 6 | 4 | ||
| 2 | 5 | 3 | 1 |
父结点均大于子节点,符合大顶堆的定义。
D
| 7 | ||
|---|---|---|
| 5 | 3 | |
| 1 | 6 | |
5作为6的父结点却小于6,所以不是大顶堆。