“有限自动机和正规式”的版本间的差异
Jihongchang(讨论 | 贡献) (建立内容为“https://www.bilibili.com/video/BV1hg411V7Bm?p=50”的新页面) |
Jihongchang(讨论 | 贡献) |
||
| (未显示同一用户的18个中间版本) | |||
| 第1行: | 第1行: | ||
https://www.bilibili.com/video/BV1hg411V7Bm?p=50 | https://www.bilibili.com/video/BV1hg411V7Bm?p=50 | ||
| + | |||
| + | === 1)正规式 === | ||
| + | 正规式:由正规文法转换而来,通常正规文法等价于正规式。 | ||
| + | {| class="wikitable" | ||
| + | ! | ||
| + | !文法产生式 | ||
| + | !正规式 | ||
| + | |- | ||
| + | !规则1 | ||
| + | |A→xB,B→y | ||
| + | |A=xy | ||
| + | |- | ||
| + | !规则2 | ||
| + | |<nowiki>A→xA|y</nowiki> | ||
| + | |A=x<sup>*</sup>y | ||
| + | |- | ||
| + | !规则3 | ||
| + | |A→x,A→y | ||
| + | |<nowiki>A=x|y</nowiki> | ||
| + | |} | ||
| + | 说明: | ||
| + | |||
| + | 规则1不难理解,由A可以推导出xB,又由B可以推导出y,那么就可以根据前面两点推导出A=xy; | ||
| + | |||
| + | |||
| + | |||
| + | 规则2:A=x<sup>*</sup>y中的“<sup>*</sup>”表示出现0次或任意次 | ||
| + | |||
| + | A→xA|y表示——由A可以推导出xA,也可以由A推导出y | ||
| + | |||
| + | 由A→y,则x出现0次; | ||
| + | |||
| + | 又由A→xA和A→y,可以得到A→xy,则x出现了1次; | ||
| + | |||
| + | 又由A→xA和A→xy,可以得到A→xxy,则x出现了2次; | ||
| + | |||
| + | ... | ||
| + | |||
| + | 又由A→x...A和A→xy,可以得到A→xx...y,则x出现了N次; | ||
| + | |||
| + | |||
| + | |||
| + | 正规集:正规文法产生的集合是语言基本字符集上的字符串的一个子集。 | ||
| + | {| class="wikitable" | ||
| + | |+ | ||
| + | !正规式 | ||
| + | !正规集 | ||
| + | ! | ||
| + | |- | ||
| + | |ab | ||
| + | |符号串ab构成的集合 | ||
| + | |a、b | ||
| + | |- | ||
| + | |<nowiki>a|b</nowiki> | ||
| + | |符号串a、b构成的集合 | ||
| + | | | ||
| + | |- | ||
| + | |a<sup>*</sup> | ||
| + | |由0个或多个a构成的符号串集合 | ||
| + | | | ||
| + | |- | ||
| + | |<nowiki>(a|b)</nowiki><sup>*</sup> | ||
| + | |所有由a和b构成的符号串集合 | ||
| + | |<nowiki>(a|b)(a|b) aa、ab、ba、bb</nowiki> | ||
| + | |- | ||
| + | |<nowiki>a(a|b)</nowiki><sup>*</sup> | ||
| + | |a为首字符的a和b构成的符号串集合 | ||
| + | | | ||
| + | |- | ||
| + | |<nowiki>(a|b)</nowiki><sup>*</sup>abc | ||
| + | |a和b构成的以abb结尾的符号串集合 | ||
| + | | | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | 表示“以字符a开头且仅由字符a、b构成的所有字符串”的正规式为()。 | ||
| + | |||
| + | A、a<sup>*</sup>b<sup>*</sup> | ||
| + | |||
| + | B、(a|b)<sup>*</sup>a | ||
| + | |||
| + | C、a(a|b)<sup>*</sup> √ | ||
| + | |||
| + | D、(ab)<sup>*</sup> | ||
| + | |||
| + | 题解: | ||
| + | |||
| + | 因为“<sup>*</sup>”表示出现0次或多次, | ||
| + | |||
| + | 那么对于选项A,如果a出现0次就变成了以字符b开头; | ||
| + | |||
| + | 对于选项B,也可以是以字符b开头, | ||
| + | |||
| + | 选项D,会是ab、abab、ababab,所以选C | ||
| + | |||
| + | |||
| + | === 2)有限自动机 === | ||
| + | [[文件:有限自动机.png|无|缩略图|600x600像素]] | ||
| + | |||
| + | |||
| + | |||
| + | 下图所示的有限自动机中,S<sub>0</sub>是初始状态,S<sub>3</sub>为终止状态,该自动机不能识别()。 | ||
| + | [[文件:有限自动机 题1.png|无|缩略图|600x600像素]] | ||
| + | A、abab √ | ||
| + | |||
| + | B、aaaa | ||
| + | |||
| + | C、babb | ||
| + | |||
| + | D、abba | ||
| + | |||
| + | 题解: | ||
| + | |||
| + | '''<big>一定要初始状态开始,终止状态结束</big>'''。 | ||
| + | |||
| + | 选项A的状态路径是S<sub>0</sub>→S<sub>1</sub>→S<sub>2</sub>→S<sub>1</sub>→S<sub>2</sub>,没有到达终止状态; | ||
| + | |||
| + | 选项B的状态路径是S<sub>0</sub>→S<sub>1</sub>→S<sub>3</sub>→S<sub>3</sub>→S<sub>3</sub>,到达终止状态结束; | ||
| + | |||
| + | 选项C的状态路径是S<sub>0</sub>→S<sub>2</sub>→S<sub>1</sub>→S<sub>2</sub>→S<sub>3</sub>,到达终止状态结束; | ||
| + | |||
| + | 选项D的状态路径是S<sub>0</sub>→S<sub>1</sub>→S<sub>2</sub>→S<sub>3</sub>→S<sub>3</sub>,到达终止状态结束; | ||
| + | |||
| + | 所以答案是选项A | ||
| + | |||
| + | |||
| + | === 考点1:正规式 === | ||
| + | 正规式(ab|c)(0|1|2)表示的正规集合中有()个元素, | ||
| + | |||
| + | A、3 | ||
| + | |||
| + | B、5 | ||
| + | |||
| + | C、6 √ | ||
| + | |||
| + | D、9 | ||
| + | |||
| + | ()是该正规集中的元素。 | ||
| + | |||
| + | A、abc012 | ||
| + | |||
| + | B、a0 | ||
| + | |||
| + | C、c02 | ||
| + | |||
| + | D、c0 √ | ||
| + | |||
| + | 题解: | ||
| + | |||
| + | 正规式(ab|c)(0|1|2)表示的正规集合是: | ||
| + | |||
| + | ab0、ab1、ab2 | ||
| + | |||
| + | c0、c1、c2 | ||
| + | |||
| + | |||
| + | === 考点2:有限自动机 === | ||
| + | 下图是一个有限自动机的状态转换图(A为初态、C为终态),该自动机识别的字符串集合可用正规式()来表示。 | ||
| + | [[文件:考点2 有限自动机.png|无|缩略图|600x600像素]] | ||
| + | A、(1|2)<sup>*</sup>00 | ||
| + | |||
| + | B、0(1|2)<sup>*</sup>0 √ | ||
| + | |||
| + | C、(0|1|2)<sup>*</sup> | ||
| + | |||
| + | D、00(1|2)<sup>*</sup> | ||
| + | |||
| + | 题解: | ||
| + | |||
| + | 注意:没有C回指B方向的线,那个箭头是2那条方向线的箭头 | ||
2022年9月16日 (五) 08:46的最新版本
https://www.bilibili.com/video/BV1hg411V7Bm?p=50
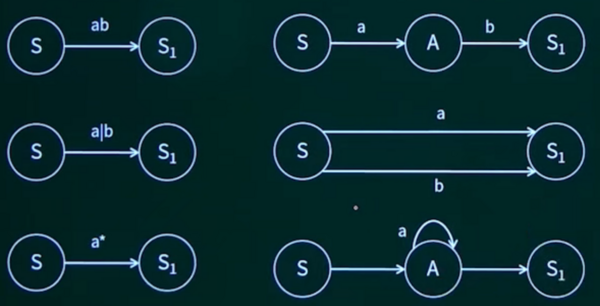
1)正规式
正规式:由正规文法转换而来,通常正规文法等价于正规式。
| 文法产生式 | 正规式 | |
|---|---|---|
| 规则1 | A→xB,B→y | A=xy |
| 规则2 | A→xA|y | A=x*y |
| 规则3 | A→x,A→y | A=x|y |
说明:
规则1不难理解,由A可以推导出xB,又由B可以推导出y,那么就可以根据前面两点推导出A=xy;
规则2:A=x*y中的“*”表示出现0次或任意次
A→xA|y表示——由A可以推导出xA,也可以由A推导出y
由A→y,则x出现0次;
又由A→xA和A→y,可以得到A→xy,则x出现了1次;
又由A→xA和A→xy,可以得到A→xxy,则x出现了2次;
...
又由A→x...A和A→xy,可以得到A→xx...y,则x出现了N次;
正规集:正规文法产生的集合是语言基本字符集上的字符串的一个子集。
| 正规式 | 正规集 | |
|---|---|---|
| ab | 符号串ab构成的集合 | a、b |
| a|b | 符号串a、b构成的集合 | |
| a* | 由0个或多个a构成的符号串集合 | |
| (a|b)* | 所有由a和b构成的符号串集合 | (a|b)(a|b) aa、ab、ba、bb |
| a(a|b)* | a为首字符的a和b构成的符号串集合 | |
| (a|b)*abc | a和b构成的以abb结尾的符号串集合 |
表示“以字符a开头且仅由字符a、b构成的所有字符串”的正规式为()。
A、a*b*
B、(a|b)*a
C、a(a|b)* √
D、(ab)*
题解:
因为“*”表示出现0次或多次,
那么对于选项A,如果a出现0次就变成了以字符b开头;
对于选项B,也可以是以字符b开头,
选项D,会是ab、abab、ababab,所以选C
2)有限自动机
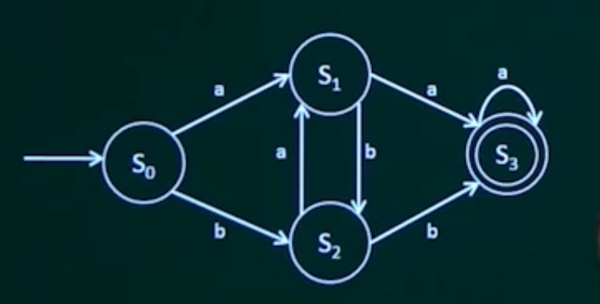
下图所示的有限自动机中,S0是初始状态,S3为终止状态,该自动机不能识别()。
A、abab √
B、aaaa
C、babb
D、abba
题解:
一定要初始状态开始,终止状态结束。
选项A的状态路径是S0→S1→S2→S1→S2,没有到达终止状态;
选项B的状态路径是S0→S1→S3→S3→S3,到达终止状态结束;
选项C的状态路径是S0→S2→S1→S2→S3,到达终止状态结束;
选项D的状态路径是S0→S1→S2→S3→S3,到达终止状态结束;
所以答案是选项A
考点1:正规式
正规式(ab|c)(0|1|2)表示的正规集合中有()个元素,
A、3
B、5
C、6 √
D、9
()是该正规集中的元素。
A、abc012
B、a0
C、c02
D、c0 √
题解:
正规式(ab|c)(0|1|2)表示的正规集合是:
ab0、ab1、ab2
c0、c1、c2
考点2:有限自动机
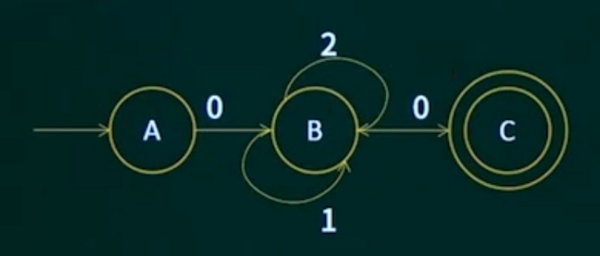
下图是一个有限自动机的状态转换图(A为初态、C为终态),该自动机识别的字符串集合可用正规式()来表示。
A、(1|2)*00
B、0(1|2)*0 √
C、(0|1|2)*
D、00(1|2)*
题解:
注意:没有C回指B方向的线,那个箭头是2那条方向线的箭头